Quantitative Data Analysis
Resources for study design through to data analysis and dissemination
Statistical analysis of quantitative data requires first choosing an appropriate method. Following analysis, results are summarized and reported in tables, charts, and graphs for interpretation, discussion, and dissemination in papers, manuscripts, and/or presentations.
UCalgary's Data Science Advisory Unit is available to help with study design, statistical analysis, visualization, and interpreting results (fee may apply).
Getting Started
Designing a study includes developing good research question(s), choosing an appropriate methodology, estimating sample size, selecting data collection tools, and creating an analysis plan.
UCalgary's Research Computing Services is available to help researchers with study design, interpretation of results, and writing up results for publication.
Your study design is guided by the research question(s). For example, does your question start with “How?” or “Why?” If so, your questions might be better addressed using qualitative methods. If you are asking “What?”, “When?, “Where?” or “How much?” you could consider quantitative methodologies. You might even combine both into a mixed methods approach.
Example Study Designs
- Descriptive (case reports, case series, descriptive surveys)
- Observational/Analytic (cross-sectional, case-control, cohort, hybrid)
- Experimental/Intervention (randomized controlled trials, quasi-experimental designs)
- Mixed Methods (quantitative and qualitative methodologies combined)
Sample size calculations are a key part of a research study. Sample size calculations should be run for each of your main/primary outcomes so you know that your study won’t be underpowered for any of the questions you plan to address.
The sample size calculation depends on your hypothesis test, the significance level (usually set as 5%), and the power and results from your pilot study. There are many formulas available for different research situations.
Another important part of study planning is selecting a sampling technique. How will you select your participants? Will it be a convenience sample? Random sample? Cluster sample? Snowball sample?
Your choice will depend on the research question(s) and study design. Note that different sampling methods have corresponding potential biases. For example, if your sample was a “convenience sample,” the results may not be generalizable or may be biased in other ways (e.g. selection bias).
The analysis plan is your road map for data management and analysis. Writing up an analysis plan is a great way to keep things on track.
Conducting a complete analysis of the data you have collected will enable you to:
- Answer your research question(s)
- Determine the impact of your work
- Have scientific validation of your work
Plans also help with timelines and standardizing analytic approaches (e.g. treatment of missing values, inclusion and exclusion criteria).
Data will have to be entered, coded and checked, new variables created, etc., even when doing secondary data analyses.
Create a data dictionary containing all of your variables, any derived variables and notes about how you coded them. This is useful not only if you will be sharing the dataset with other, but for yourself (e.g., if you need to come back to the data after some time away). Keep in mind that data cleaning is a process that will likely involve you revisiting the data several times over.
Learn more
Types of Data
Primary data: data that you collect yourself from participants or health records using surveys, chart reviews, interviews, focus groups, etc.
Secondary data: data collected by other researchers that you are using to answer your own research questions
Qualitative vs. Quantitative Data
The type of data you collect depends on the question you want to answer and your resources. Both quantitative and qualitative data have strengths and limitations and may be appropriate for different settings, evaluation designs, and evaluation questions.
Qualitative data consist of words and narratives. The analysis of qualitative data can come in many forms including highlighting key words, extracting themes, and elaborating on concepts.
Quantitative data are numerical information, the analysis of which involves statistical techniques. The type of data you collect guides the analysis process.
Types of Variables
Dependent (Outcome) variables are the outcome of interest and will answer your research question(s).
Independent (Predictor) variables are those factors that may influence your dependent variable/outcome variable.
Example: Say you’re conducting a study on diet and exercise. Your weight would be your dependent variable and your diet and exercise (which both influence weight) would be your independent variables.
Categorical vs. Continuous Variables
Categorical variables are based on groupings or classification. There are two types: Nominal (no inherent order) and Ordinal (natural order).
Nominal Example – Smoker vs. Non-Smoker
Ordinal Example – Educational Level (Less than High School, High School, Some College, College, Bachelor’s Degree, Graduate Degree)
Continuous variables can take on any score or value within a measurement scale. There are two types: Interval and Ratio Scale. An interval variable can be ordered, and the distance or level between each category is equal and static. A ratio scale variable is similar to an interval variable with one difference: the ratio scale has true zero point (i.e., 0.0 = none/absence of the measurement).
Interval Example – Temperature
Ratio Scale Example – Weight
Learn more
Descriptive Statistics
Descriptive statistics are commonly used to describe and explore quantitative datasets.
Before proceeding, you should assess the distribution of your data and consider variable transformations or non-parametric options, if necessary. It’s also a good idea to identify missing data and start thinking about how you might want to handle this (e.g. listwise deletion, imputation).
Common Descriptive Statistics
- Minimum (Min): lowest/smallest score in a data set
- Maximum (Max): highest/largest score in a data set
- Frequency: number of times a certain score appears in a data set
- Mean (Average): sum of all the scores divided by the number of scores
- Median: middle score of a data set after values ordered numerically; it divides the distribution in half
- Mode: most frequently occurring score in a data set
- Standard Deviation (SD): represents the average amount that a given score deviates from the mean score
Learn more
Hypothesis Testing
Data and Normality
The goal of estimation and hypothesis testing is to generalize the results from a sample to the population. We need to determine whether a pattern we observe in the sample is due to chance or due to program or intervention effects.
Inferential analysis is used to determine if there is a relationship between an intervention or program and an outcome, as well as the strength of that relationship. The type of test selected for inferential analysis should be guided by the distribution of your data. Is it a normal or non-normal distribution?
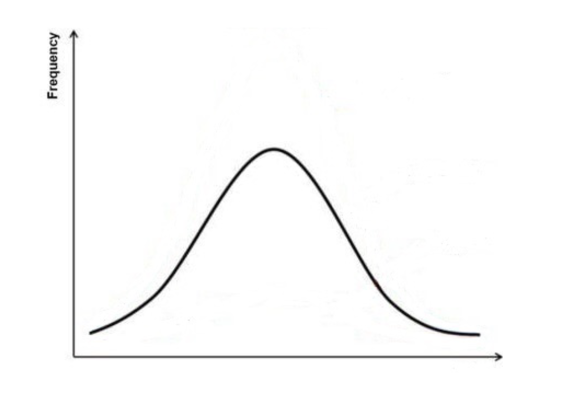
Normal Distribution
A normal distribution looks like a Bell Curve (right).
Looking at your distribution, draw a curve over it that most closely fits your data. If your curve closely resembles the one in the image, your distribution is normal.
In a normal distribution the majority of the data is clustered around one number or value. If the data is normal, we usually choose a parametric statistical test for data analysis.
Non-Normal Distributions
There are several reasons that a distribution may be non-normal. A small sample size or unusual sets of responses are common reasons that data may not be normally distributed. If the data is non-normal, we usually choose from a set of statistical tests called non-parametric statistical tests.
Non-normal data will have issues with skewness and/or kurtosis (below).
Negative Skew
The graph shows negatively skewed data; the majority of the scores are at the higher end of possible scores. The curve has a longer curve to the left.
Positive Skew
The graph shows positively skewed data; the majority of the scores are at the lower end of possible scores. The curve has a longer curve to the right.
Kurtosis
This graph illustrates kurtosis, the spread or ‘peakedness’ of the distribution. A distribution can be too peaked or pointy.
Choosing a Statistical Test
Statistical tests allow us to make inferences about a sample because they can validate if the differences, associations, and patterns that we detect are real and not due to chance.
Selecting the appropriate test depends on the research design, the type of variable, and the distribution of the data.
If the data is normally distributed, you will choose a type of parametric test. If normality is violated, then you will need to use a test that doesn’t need the normality assumption to be valid. We call these non-parametric tests or parametric-independent tests.
SAGE Research provides an online tool to help you decide which test to choose.
Learn more
Sample Size & Power
Sample size calculations should be run for each of your primary outcomes so that your study won't be underpowered for any of the research questions that you plan to address. *For surveys, Qualtrics has a sample size calculator.
Before calculating sample size, ask yourself:
1. Is my study descriptive or comparative?
2. Is(are) the primary outcome variable(s) continuous or categorical?
Descriptive Studies
Use the Confidence Interval Approach
Use this approach to estimate your sample size when you want an interval around an estimate with a certain confidence level.
Example
The population prevalence of hypertension among Canadians aged 20 to 79 was found to be significantly higher for men (24.5%, 95% CI : 22.7% to 26.4%) than for women (21.5%, 95% CI : 19.8% to 23.2%). Statistics Canada
Therefore, for men, point estimate is 24.5%, the margin of error is 1.9%.
Comparative Studies
Use the Hypothesis Testing Approach
Use this approach to estimate your sample size so that if such a difference exists, then findings would be statistically significant. The information you need to calculate a sample size will vary according to your study design, research questions, analysis plan and study restrictions. Prior to the calculation, you will need to decide on your:
Power. This is the ability of the statistical test to detect differences or effects that lead to rejection of the null hypothesis. It depends on the sample size. The larger the sample size, the bigger the power. It is important to calculate the sample size to have sufficient power before you begin your data collection. When your sample size is small, your study might not be able to detect the difference or effect, even when it is real, because of lack of power. Power is usually set at 80-90% power.
Level of significance (α). This is the pre-set level of error that you want to commit in your research, determined before your data collection. It is usually set at 0.05 or 0.01. P-value is the actual level of error found when you perform the statistical test. When p-value < α, then it supports the evidence against the null hypothesis (no effect) and your results are ‘statistically significant’.
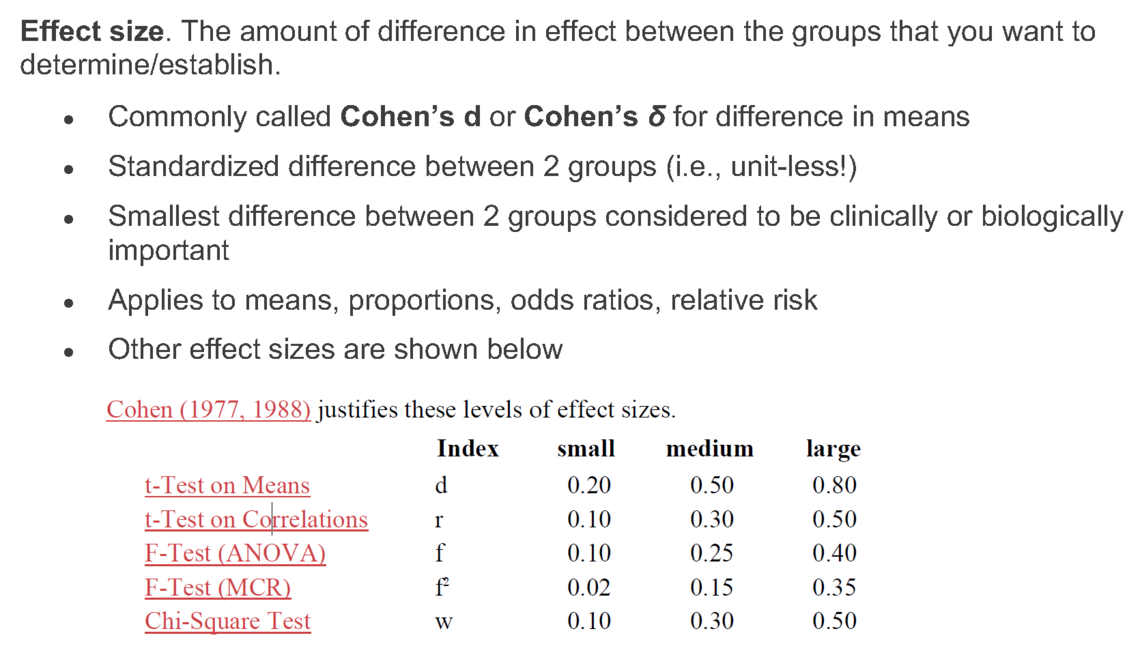
Learn more
Interpreting Results
In the results section you report on just the objective “facts and figures” of what you found. You then interpret these results in the discussion section.
UCalgary's Research Computing Services is available to help researchers with study design, interpretation of results, and writing up results for publication.
You have to report the results of your project or study in relation to your research questions/hypothesis. Present the results of the outcome variable(s) for each hypothesis.
Some guiding questions to consider when explaining your results:
- Do the results agree with the ideas that you introduced in your proposal?
- How do the results relate to previous literature or current theory?
- Discuss any of the limitations in the study design that may reduce the strength of your results.
Use descriptive language to indicate the strength of the evidence.
p-value, Description
< 0.001, Extremely significant; Very strong evidence against the null hypothesis in favor of the alternative
0.001 – 0.010, Highly significant; Strong evidence against the null hypothesis in favor of the alternative
0.011 – 0.050, Significant; Moderate evidence against the null hypothesis in favor of the alternative
0.051 – 0.100, Not significant; Weak evidence against the null hypothesis in favor of the alternative
> 0.100, No evidence; No evidence against the null hypothesis
This is where you explain the extent to which your study is externally valid. Discuss strengths and weaknesses of applying your results to, e.g., another population, species, age, or sex.
Based on your results, and considering the study's limitations, introduce new ideas or ways to improve the current area of research.
Try to identify and discuss factors or conditions that may have contributed to unexpected results. For example, site conditions (e.g., room temperature) could have been different between two focus group sessions.
Be careful about drawing erroneous conclusions. Report only actual findings and the relationships and associations between outcomes and predictor variables that have been confirmed with statistical evidence. For example, just because you find that two variables are related, you cannot automatically leap to the conclusion that those two variables have a cause-and-effect relationship.
Refrain from generalizing your results to a larger group than was actually represented by your study. For example, results from a study involving nursing students may not be applicable to registered nurses.
Resist the temptation to deviate or to make sweeping generalities based on your findings.
Summarize the study’s strengths, conclusions, implications, and your suggestions for future research.
Learn more
Reporting Results
The Results section of your paper should only be used to report, not interpret, your findings. The Discussion section is where the interpretation and implications of your findings are presented.
UCalgary's Research Computing Services is available to help researchers with study design, interpretation of results, and writing up results for publication.
The American Psychological Association (APA) style guide is most commonly used within the social sciences.
Best Practices for Reporting
1. Summarize succinctly.
The Results section is the shortest and most condensed section in a manuscript or thesis/dissertation, typically 1-2 pages. Present each of your variables in separate subsections, writing a brief summary for each.
2. Keep the 'Results' and 'Discussion' sections separate.
Statistical results are presented but are not discussed in the results section. Reserve your interpretation for the discussion section.
3. Provide the results separately for each hypotheses.
The Results section should describe how your data supports or refutes each hypothesis.
4. Include tables and figures.
Using tables and figures is a great way to summarize your results. Include descriptive statistics (such as means and standard deviations) and/or the results of any inferential statistics (test statistic, degrees of freedom, confidence intervals, and the p-value).
5. Be careful when drawing conclusions.
Draw appropriate conclusions from your findings. Do not overstate the importance of results and limit your conclusions to the population that is actually represented by your study.